In mathematics, Itô's lemma or Itô's formula (also called the Itô–Doeblin formula, especially in the French literature) is an identity used in Itô calculus to find the differential of a time-dependent function of a stochastic process. It serves as the stochastic calculus counterpart of the chain rule. It can be heuristically derived by forming the Taylor series expansion of the function up to its second derivatives and retaining terms up to first order in the time increment and second order in the Wiener process increment. The lemma is widely employed in mathematical finance, and its best known application is in the derivation of the Black–Scholes equation for option values.
Kiyoshi Itô published a proof of the formula in 1951.[1]
Motivation
Suppose we are given the stochastic differential equation where Bt is a Wiener process and the functions are deterministic (not stochastic) functions of time. In general, it's not possible to write a solution directly in terms of However, we can formally write an integral solution
This expression lets us easily read off the mean and variance of (which has no higher moments). First, notice that every individually has mean 0, so the expected value of is simply the integral of the drift function:
Similarly, because the terms have variance 1 and no correlation with one another, the variance of is simply the integral of the variance of each infinitesimal step in the random walk:
However, sometimes we are faced with a stochastic differential equation for a more complex process in which the process appears on both sides of the differential equation. That is, say for some functions and In this case, we cannot immediately write a formal solution as we did for the simpler case above. Instead, we hope to write the process as a function of a simpler process taking the form above. That is, we want to identify three functions and such that and In practice, Ito's lemma is used in order to find this transformation. Finally, once we have transformed the problem into the simpler type of problem, we can determine the mean and higher moments of the process.
Informal derivation
A formal proof of the lemma relies on taking the limit of a sequence of random variables. This approach is not presented here since it involves a number of technical details. Instead, we give a sketch of how one can derive Itô's lemma by expanding a Taylor series and applying the rules of stochastic calculus.
Suppose Xt is an Itô drift-diffusion process that satisfies the stochastic differential equation
where Bt is a Wiener process.
If f(t,x) is a twice-differentiable scalar function, its expansion in a Taylor series is
Substituting Xt for x and therefore μt dt + σt dBt for dx gives
In the limit dt → 0, the terms dt2 and dt dBt tend to zero faster than dB2, which is O(dt). Setting the dt2 and dt dBt terms to zero, substituting dt for dB2 (due to the quadratic variation of a Wiener process), and collecting the dt and dB terms, we obtain
as required.
Geometric intuition
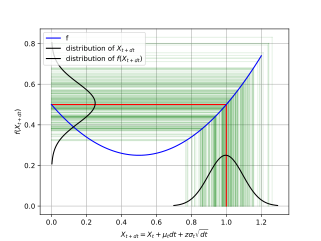
Suppose we know that are two jointly-Gaussian distributed random variables, and is nonlinear but has continuous second derivative, then in general, neither of is Gaussian, and their joint distribution is also not Gaussian. However, since is Gaussian, we might still find is Gaussian. This is not true when is finite, but when becomes infinitesimal, this becomes true.
The key idea is that has a deterministic part and a noisy part. When is nonlinear, the noisy part has a deterministic contribution. If is convex, then the deterministic contribution is positive (by Jensen's inequality).
To find out how large the contribution is, we write , where is a standard Gaussian, then perform Taylor expansion. We have split it into two parts, a deterministic part, and a random part with mean zero. The random part is non-Gaussian, but the non-Gaussian parts decay faster than the Gaussian part, and at the limit, only the Gaussian part remains. The deterministic part has the expected , but also a part contributed by the convexity: .
To understand why there should be a contribution due to convexity, consider the simplest case of geometric Brownian walk (of the stock market): . In other words, . Let , then , and is a Brownian walk. However, although the expectation of remains constant, the expectation of grows. Intuitively it is because the downside is limited at zero, but the upside is unlimited. That is, while is normally distributed, is log-normally distributed.
Mathematical formulation of Itô's lemma
In the following subsections we discuss versions of Itô's lemma for different types of stochastic processes.
Itô drift-diffusion processes (due to: Kunita–Watanabe)
In its simplest form, Itô's lemma states the following: for an Itô drift-diffusion process
and any twice differentiable scalar function f(t,x) of two real variables t and x, one has
This immediately implies that f(t,Xt) is itself an Itô drift-diffusion process.
In higher dimensions, if is a vector of Itô processes such that
for a vector and matrix , Itô's lemma then states that
where is the gradient of f w.r.t. X, HX f is the Hessian matrix of f w.r.t. X, and Tr is the trace operator.
Poisson jump processes
We may also define functions on discontinuous stochastic processes.
Let h be the jump intensity. The Poisson process model for jumps is that the probability of one jump in the interval [t, t + Δt] is hΔt plus higher order terms. h could be a constant, a deterministic function of time, or a stochastic process. The survival probability ps(t) is the probability that no jump has occurred in the interval [0, t]. The change in the survival probability is
So
Let S(t) be a discontinuous stochastic process. Write for the value of S as we approach t from the left. Write for the non-infinitesimal change in S(t) as a result of a jump. Then
Let z be the magnitude of the jump and let be the distribution of z. The expected magnitude of the jump is
Define , a compensated process and martingale, as
Then
Consider a function of the jump process dS(t). If S(t) jumps by Δs then g(t) jumps by Δg. Δg is drawn from distribution which may depend on , dg and . The jump part of is
If contains drift, diffusion and jump parts, then Itô's Lemma for is
Itô's lemma for a process which is the sum of a drift-diffusion process and a jump process is just the sum of the Itô's lemma for the individual parts.
Non-continuous semimartingales
Itô's lemma can also be applied to general d-dimensional semimartingales, which need not be continuous. In general, a semimartingale is a càdlàg process, and an additional term needs to be added to the formula to ensure that the jumps of the process are correctly given by Itô's lemma. For any cadlag process Yt, the left limit in t is denoted by Yt−, which is a left-continuous process. The jumps are written as ΔYt = Yt − Yt−. Then, Itô's lemma states that if X = (X1, X2, ..., Xd) is a d-dimensional semimartingale and f is a twice continuously differentiable real valued function on Rd then f(X) is a semimartingale, and
This differs from the formula for continuous semi-martingales by the additional term summing over the jumps of X, which ensures that the jump of the right hand side at time t is Δf(Xt).
Multiple non-continuous jump processes
[citation needed]There is also a version of this for a twice-continuously differentiable in space once in time function f evaluated at (potentially different) non-continuous semi-martingales which may be written as follows:
where denotes the continuous part of the ith semi-martingale.
Examples
Geometric Brownian motion
A process S is said to follow a geometric Brownian motion with constant volatility σ and constant drift μ if it satisfies the stochastic differential equation , for a Brownian motion B. Applying Itô's lemma with gives
It follows that
exponentiating gives the expression for S,
The correction term of − σ2/2 corresponds to the difference between the median and mean of the log-normal distribution, or equivalently for this distribution, the geometric mean and arithmetic mean, with the median (geometric mean) being lower. This is due to the AM–GM inequality, and corresponds to the logarithm being concave (or convex upwards), so the correction term can accordingly be interpreted as a convexity correction. This is an infinitesimal version of the fact that the annualized return is less than the average return, with the difference proportional to the variance. See geometric moments of the log-normal distribution for further discussion.
The same factor of σ2/2 appears in the d1 and d2 auxiliary variables of the Black–Scholes formula, and can be interpreted as a consequence of Itô's lemma.
Doléans-Dade exponential
The Doléans-Dade exponential (or stochastic exponential) of a continuous semimartingale X can be defined as the solution to the SDE dY = Y dX with initial condition Y0 = 1. It is sometimes denoted by Ɛ(X). Applying Itô's lemma with f(Y) = log(Y) gives
Exponentiating gives the solution
Black–Scholes formula
Itô's lemma can be used to derive the Black–Scholes equation for an option.[2] Suppose a stock price follows a geometric Brownian motion given by the stochastic differential equation dS = S(σdB + μ dt). Then, if the value of an option at time t is f(t, St), Itô's lemma gives
The term ∂f/∂S dS represents the change in value in time dt of the trading strategy consisting of holding an amount ∂ f/∂S of the stock. If this trading strategy is followed, and any cash held is assumed to grow at the risk free rate r, then the total value V of this portfolio satisfies the SDE
This strategy replicates the option if V = f(t,S). Combining these equations gives the celebrated Black–Scholes equation
Product rule for Itô processes
Let be a two-dimensional Ito process with SDE:
Then we can use the multi-dimensional form of Ito's lemma to find an expression for .
We have and .
We set and observe that and
Substituting these values in the multi-dimensional version of the lemma gives us:
This is a generalisation of Leibniz's product rule to Ito processes, which are non-differentiable.
Further, using the second form of the multidimensional version above gives us
so we see that the product is itself an Itô drift-diffusion process.
Itô's formula for functions with finite quadratic variation
An idea by Hans Föllmer was to extend Itô's formula to functions with finite quadratic variation.[3]
Let be a real-valued function and a RCLL function with finite quadratic variation. Then
Infinite-dimensional formulas
There exist a couple of extensions to infinite-dimensional spaces (e.g. Pardoux,[4] Gyöngy-Krylov,[5] Brzezniak-van Neerven-Veraar-Weis[6]).
See also
Notes
- ^ Itô, Kiyoshi (1951). "On a formula concerning stochastic differentials". Nagoya Math. J. 3: 55–65. doi:10.1017/S0027763000012216.
- ^ Malliaris, A. G. (1982). Stochastic Methods in Economics and Finance. New York: North-Holland. pp. 220–223. ISBN 0-444-86201-3.
- ^ Föllmer, Hans (1981). "Calcul d'Ito sans probabilités". Séminaire de probabilités de Strasbourg. 15: 143–144.
- ^ Pardoux, Étienne (1974). "Équations aux dérivées partielles stochastiques de type monotone". Séminaire Jean Leray (3).
- ^ Gyöngy, István; Krylov, Nikolay Vladim Vladimirovich (1981). "Ito formula in banach spaces". In M. Arató; D. Vermes, D.; A.V. Balakrishnan (eds.). Stochastic Differential Systems. Lecture Notes in Control and Information Sciences. Vol. 36. Springer, Berlin, Heidelberg. pp. 69–73. doi:10.1007/BFb0006409. ISBN 3-540-11038-0.
- ^ Brzezniak, Zdzislaw; van Neerven, Jan M. A. M.; Veraar, Mark C.; Weis, Lutz (2008). "Ito's formula in UMD Banach spaces and regularity of solutions of the Zakai equation". Journal of Differential Equations. 245 (1): 30–58. arXiv:0804.0302. doi:10.1016/j.jde.2008.03.026.
References
- Kiyosi Itô (1944). Stochastic Integral. Proc. Imperial Acad. Tokyo 20, 519–524. This is the paper with the Ito Formula; Online
- Kiyosi Itô (1951). On stochastic differential equations. Memoirs, American Mathematical Society 4, 1–51. Online
- Bernt Øksendal (2000). Stochastic Differential Equations. An Introduction with Applications, 5th edition, corrected 2nd printing. Springer. ISBN 3-540-63720-6. Sections 4.1 and 4.2.
- Philip E Protter (2005). Stochastic Integration and Differential Equations, 2nd edition. Springer. ISBN 3-662-10061-4. Section 2.7.
External links
- Derivation, Prof. Thayer Watkins
- Informal proof, optiontutor







![{\displaystyle \mathrm {E} [X_{t}]=\int _{0}^{t}\mu _{s}\ ds.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e53226b7178e001e4637aca15af9333ffc657b1)

![{\displaystyle \mathrm {Var} [X_{t}]=\int _{0}^{t}\sigma _{s}^{2}\ ds.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89bbb1ad99a2a0e0b9e5a6ab3102ce4d7506699d)















![{\displaystyle E[f(X_{t+dt})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3847d540a61535c2453b66574c61361389ac302d)
![{\displaystyle f(E[X_{t+dt}])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0fa1226c75ef2dbab8e442fca344fd4cf0502026)
![{\displaystyle f''(E[X_{t+dt}])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d9dddbaa488acef1bf96b7fe890905d6beb5f92)
























![{\displaystyle {\begin{aligned}df(t,\mathbf {X} _{t})&={\frac {\partial f}{\partial t}}\,dt+\left(\nabla _{\mathbf {X} }f\right)^{T}\,d\mathbf {X} _{t}+{\frac {1}{2}}\left(d\mathbf {X} _{t}\right)^{T}\left(H_{\mathbf {X} }f\right)\,d\mathbf {X} _{t},\\[4pt]&=\left\{{\frac {\partial f}{\partial t}}+\left(\nabla _{\mathbf {X} }f\right)^{T}{\boldsymbol {\mu }}_{t}+{\frac {1}{2}}\operatorname {Tr} \left[\mathbf {G} _{t}^{T}\left(H_{\mathbf {X} }f\right)\mathbf {G} _{t}\right]\right\}\,dt+\left(\nabla _{\mathbf {X} }f\right)^{T}\mathbf {G} _{t}\,d\mathbf {B} _{t}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9ff5de07176d12bde24e628b9ff26bf5fe27767)







![{\displaystyle E[d_{j}S(t)]=h(S(t^{-}))\,dt\int _{z}z\eta (S(t^{-}),z)\,dz.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9810f5bac71e8426f2ce24e1fc3e1d464c6b291f)

![{\displaystyle dJ_{S}(t)=d_{j}S(t)-E[d_{j}S(t)]=S(t)-S(t^{-})-\left(h(S(t^{-}))\int _{z}z\eta \left(S(t^{-}),z\right)\,dz\right)\,dt.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46d946d57485a9ac35874f5b482b24f51b5c56a5)
![{\displaystyle d_{j}S(t)=E[d_{j}S(t)]+dJ_{S}(t)=h(S(t^{-}))\left(\int _{z}z\eta (S(t^{-}),z)\,dz\right)dt+dJ_{S}(t).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04a1543f9dff897cb7519f50a2022bef0b922b19)







![{\displaystyle {\begin{aligned}f(X_{t})&=f(X_{0})+\sum _{i=1}^{d}\int _{0}^{t}f_{i}(X_{s-})\,dX_{s}^{i}+{\frac {1}{2}}\sum _{i,j=1}^{d}\int _{0}^{t}f_{i,j}(X_{s-})\,d[X^{i},X^{j}]_{s}\\&\qquad +\sum _{s\leq t}\left(\Delta f(X_{s})-\sum _{i=1}^{d}f_{i}(X_{s-})\,\Delta X_{s}^{i}-{\frac {1}{2}}\sum _{i,j=1}^{d}f_{i,j}(X_{s-})\,\Delta X_{s}^{i}\,\Delta X_{s}^{j}\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/972546c08345cc27369b206891c53006b1bf20dc)
![{\displaystyle {\begin{aligned}f(t,X_{t}^{1},\ldots ,X_{t}^{d})={}&f(0,X_{0}^{1},\ldots ,X_{0}^{d})+\int _{0}^{t}{\dot {f}}({s_{-}},X_{s_{-}}^{1},\ldots ,X_{s_{-}}^{d})d{s}\\&{}+\sum _{i=1}^{d}\int _{0}^{t}f_{i}({s_{-}},X_{s_{-}}^{1},\ldots ,X_{s_{-}}^{d})\,dX_{s}^{(c,i)}\\&{}+{\frac {1}{2}}\sum _{i_{1},\ldots ,i_{d}=1}^{d}\int _{0}^{t}f_{i_{1},\ldots ,i_{d}}({s_{-}},X_{s_{-}}^{1},\ldots ,X_{s_{-}}^{d})\,dX_{s}^{(c,i_{1})}\cdots X_{s}^{(c,i_{d})}\\&{}+\sum _{0<s\leq t}\left[f(s,X_{s}^{1},\ldots ,X_{s}^{d})-f({s_{-}},X_{s_{-}}^{1},\ldots ,X_{s_{-}}^{d})\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c62cb8fb702a30fd5f6332ed5077c54bcbb5d7b)



![{\displaystyle {\begin{aligned}df&=f^{\prime }(S_{t})\,dS_{t}+{\frac {1}{2}}f^{\prime \prime }(S_{t})(dS_{t})^{2}\\[4pt]&={\frac {1}{S_{t}}}\,dS_{t}+{\frac {1}{2}}(-S_{t}^{-2})(S_{t}^{2}\sigma ^{2}\,dt)\\[4pt]&={\frac {1}{S_{t}}}\left(\sigma S_{t}\,dB_{t}+\mu S_{t}\,dt\right)-{\frac {1}{2}}\sigma ^{2}\,dt\\[4pt]&=\sigma \,dB_{t}+\left(\mu -{\tfrac {\sigma ^{2}}{2}}\right)\,dt.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9adcd4ce799752d572f99d94b8bfc5d1a047cf2e)


![{\displaystyle {\begin{aligned}d\log(Y)&={\frac {1}{Y}}\,dY-{\frac {1}{2Y^{2}}}\,d[Y]\\[6pt]&=dX-{\tfrac {1}{2}}\,d[X].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30b6e179c463c7572e04b7d86e6cfe4c290b156e)
![{\displaystyle Y_{t}=\exp \left(X_{t}-X_{0}-{\tfrac {1}{2}}[X]_{t}\right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b4dec2eba6dbc782b7c54f9604a090fbb54091b)












![{\displaystyle {\begin{aligned}d(X_{t}^{1}X_{t}^{2})&=\left\{0+(X_{t}^{2}\ \ X_{t}^{1}){\begin{pmatrix}\mu _{t}^{1}\\\mu _{t}^{2}\end{pmatrix}}+{\frac {1}{2}}\operatorname {Tr} \left[(\sigma _{t}^{1}\ \ \sigma _{t}^{2}){\begin{pmatrix}0&1\\1&0\end{pmatrix}}{\begin{pmatrix}\sigma _{t}^{1}\\\sigma _{t}^{2}\end{pmatrix}}\right]\right\}\,dt+(X_{t}^{2}\sigma _{t}^{1}+X_{t}^{1}\sigma _{t}^{2})\,dB_{t}\\[5pt]&=\left(X_{t}^{2}\mu _{t}^{1}+X_{t}^{1}\mu _{t}^{2}+\sigma _{t}^{1}\sigma _{t}^{2}\right)\,dt+(X_{t}^{2}\sigma _{t}^{1}+X_{t}^{1}\sigma _{t}^{2})\,dB_{t}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ece13972b635cbe8063157d70fae05f4b241c08)


![{\displaystyle x:[0,\infty ]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c769f1011d128589efa9cc27ee54194f7e61849f)
![{\displaystyle {\begin{aligned}f(x_{t})={}&f(x_{0})+\int _{0}^{t}f'(x_{s-})\,\mathrm {d} x_{s}+{\frac {1}{2}}\int _{]0,t]}f''(x_{s-})\,d[x,x]_{s}\\&+\sum _{0\leq s\leq t}\left(f(x_{s})-f(x_{s-})-f'(x_{s-})\Delta x_{s}-{\frac {1}{2}}f''(x_{s-})(\Delta x_{s})^{2})\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61d8b84c9ccc23836a6a9b70ce8a2020f1209f4f)
