An interest rate is the amount of interest due per period, as a proportion of the amount lent, deposited, or borrowed (called the principal sum). The total interest on an amount lent or borrowed depends on the principal sum, the interest rate, the compounding frequency, and the length of time over which it is lent, deposited, or borrowed.
The annual interest rate is the rate over a period of one year. Other interest rates apply over different periods, such as a month or a day, but they are usually annualized.
The interest rate has been characterized as "an index of the preference . . . for a dollar of present [income] over a dollar of future income."[1] The borrower wants, or needs, to have money sooner, and is willing to pay a fee—the interest rate—for that privilege.
Influencing factors
Interest rates vary according to:
- the government's directives to the central bank to accomplish the government's goals
- the currency of the principal sum lent or borrowed
- the term to maturity of the investment
- the perceived default probability of the borrower
- supply and demand in the market
- the amount of collateral
- special features like call provisions
- reserve requirements
- compensating balance
as well as other factors.
Example
A company borrows capital from a bank to buy assets for its business. In return, the bank charges the company interest. (The lender might also require rights over the new assets as collateral.)
A bank will use the capital deposited by individuals to make loans to their clients. In return, the bank should pay interest to individuals who have deposited their capital. The amount of interest payment depends on the interest rate and the amount of capital they deposited.
Related terms
Base rate usually refers to the annualized effective interest rate offered on overnight deposits by the central bank or other monetary authority.[citation needed]
The annual percentage rate (APR) may refer either to a nominal APR or an effective APR (EAPR). The difference between the two is that the EAPR accounts for fees and compounding, while the nominal APR does not.
The annual equivalent rate (AER), also called the effective annual rate, is used to help consumers compare products with different compounding frequencies on a common basis, but does not account for fees.
A discount rate[2] is applied to calculate present value.
For an interest-bearing security, coupon rate is the ratio of the annual coupon amount (the coupon paid per year) per unit of par value, whereas current yield is the ratio of the annual coupon divided by its current market price. Yield to maturity is a bond's expected internal rate of return, assuming it will be held to maturity, that is, the discount rate which equates all remaining cash flows to the investor (all remaining coupons and repayment of the par value at maturity) with the current market price.
Based on the banking business, there are deposit interest rate and loan interest rate.
Based on the relationship between supply and demand of market interest rate, there are fixed interest rate and floating interest rate.
Monetary policy
Interest rate targets are a vital tool of monetary policy and are taken into account when dealing with variables like investment, inflation, and unemployment. The central banks of countries generally tend to reduce interest rates when they wish to increase investment and consumption in the country's economy. However, a low interest rate as a macro-economic policy can be risky and may lead to the creation of an economic bubble, in which large amounts of investments are poured into the real-estate market and stock market. In developed economies, interest-rate adjustments are thus made to keep inflation within a target range for the health of economic activities or cap the interest rate concurrently with economic growth to safeguard economic momentum.[3][4][5][6][7]
History
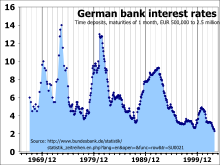
In the past two centuries, interest rates have been variously set either by national governments or central banks. For example, the Federal Reserve federal funds rate in the United States has varied between about 0.25% and 19% from 1954 to 2008, while the Bank of England base rate varied between 0.5% and 15% from 1989 to 2009,[8][9] and Germany experienced rates close to 90% in the 1920s down to about 2% in the 2000s.[10][11] During an attempt to tackle spiraling hyperinflation in 2007, the Central Bank of Zimbabwe increased interest rates for borrowing to 800%.[12]
The interest rates on prime credits in the late 1970s and early 1980s were far higher than had been recorded – higher than previous US peaks since 1800, than British peaks since 1700, or than Dutch peaks since 1600; "since modern capital markets came into existence, there have never been such high long-term rates" as in this period.[13]
Possibly before modern capital markets, there have been some accounts that savings deposits could achieve an annual return of at least 25% and up to as high as 50%. (William Ellis and Richard Dawes, "Lessons on the Phenomenon of Industrial Life... ", 1857, p III–IV)
Reasons for changes
- Political short-term gain: Lowering interest rates can give the economy a short-run boost. Under normal conditions, most economists think a cut in interest rates will only give a short term gain in economic activity that will soon be offset by inflation. The quick boost can influence elections. Most economists advocate independent central banks to limit the influence of politics on interest rates.
- Deferred consumption: When money is loaned the lender delays spending the money on consumption goods. Since according to time preference theory people prefer goods now to goods later, in a free market there will be a positive interest rate.
- Inflationary expectations: Most economies generally exhibit inflation, meaning a given amount of money buys fewer goods in the future than it will now. The borrower needs to compensate the lender for this.
- Alternative investments: The lender has a choice between using his money in different investments. If he chooses one, he forgoes the returns from all the others. Different investments effectively compete for funds.
- Risks of investment: There is always a risk that the borrower will go bankrupt, abscond, die, or otherwise default on the loan. This means that a lender generally charges a risk premium to ensure that, across his investments, he is compensated for those that fail.
- Liquidity preference: People prefer to have their resources available in a form that can immediately be exchanged, rather than a form that takes time to realize.
- Taxes: Because some of the gains from interest may be subject to taxes, the lender may insist on a higher rate to make up for this loss.
- Banks: Banks can tend to change the interest rate to either slow down or speed up economy growth. This involves either raising interest rates to slow the economy down, or lowering interest rates to promote economic growth.[14]
- Economy: Interest rates can fluctuate according to the status of the economy. It will generally be found that if the economy is strong then the interest rates will be high, if the economy is weak the interest rates will be low.
Real versus nominal
The nominal interest rate is the rate of interest with no adjustment for inflation.
For example, suppose someone deposits $100 with a bank for one year, and they receive interest of $10 (before tax), so at the end of the year, their balance is $110 (before tax). In this case, regardless of the rate of inflation, the nominal interest rate is 10% per annum (before tax).
The real interest rate measures the growth in real value of the loan plus interest, taking inflation into account. The repayment of principal plus interest is measured in real terms compared against the buying power of the amount at the time it was borrowed, lent, deposited or invested.
If inflation is 10%, then the $110 in the account at the end of the year has the same purchasing power (that is, buys the same amount) as the $100 had a year ago. The real interest rate is zero in this case.
The real interest rate is given by the Fisher equation:
where p is the inflation rate. For low rates and short periods, the linear approximation applies:
The Fisher equation applies both ex ante and ex post. Ex ante, the rates are projected rates, whereas ex post, the rates are historical.
Market rates
There is a market for investments, including the money market, bond market, stock market, and currency market as well as retail banking.
Interest rates reflect:
- The risk-free cost of capital
- Expected inflation
- Risk premium
- Transaction costs
Inflationary expectations
According to the theory of rational expectations, borrowers and lenders form an expectation of inflation in the future. The acceptable nominal interest rate at which they are willing and able to borrow or lend includes the real interest rate they require to receive, or are willing and able to pay, plus the rate of inflation they expect.
Risk
The level of risk in investments is taken into consideration. Riskier investments such as shares and junk bonds are normally expected to deliver higher returns than safer ones like government bonds.
The additional return above the risk-free nominal interest rate which is expected from a risky investment is the risk premium. The risk premium an investor requires on an investment depends on the risk preferences of the investor. Evidence suggests that most lenders are risk-averse.[15]
A maturity risk premium applied to a longer-term investment reflects a higher perceived risk of default.
There are four kinds of risk:
- repricing risk
- basis risk
- yield curve risk
- optionality
Liquidity preference
Most investors prefer their money to be in cash rather than in less fungible investments. Cash is on hand to be spent immediately if the need arises, but some investments require time or effort to transfer into spendable form. The preference for cash is known as liquidity preference. A 1-year loan, for instance, is very liquid compared to a 10-year loan. A 10-year US Treasury bond, however, is still relatively liquid because it can easily be sold on the market.
A market model
A basic interest rate pricing model for an asset is
where
- in is the nominal interest rate on a given investment
- ir is the risk-free return to capital
- i*n is the nominal interest rate on a short-term risk-free liquid bond (such as U.S. Treasury bills).
- rp is a risk premium reflecting the length of the investment and the likelihood the borrower will default
- lp is a liquidity premium (reflecting the perceived difficulty of converting the asset into money and thus into goods).
- pe is the expected inflation rate.
Assuming perfect information, pe is the same for all participants in the market, and the interest rate model simplifies to
Spread
The spread of interest rates is the lending rate minus the deposit rate.[16] This spread covers operating costs for banks providing loans and deposits. A negative spread is where a deposit rate is higher than the lending rate.[17]
In macroeconomics
Output, unemployment and inflation
Interest rates affect economic activity broadly, which is the reason why they are normally the main instrument of the monetary policies conducted by central banks.[18] Changes in interest rates will affect firms' investment behaviour, either raising or lowering the opportunity cost of investing. Interest rate changes also affect asset prices like stock prices and house prices, which again influence households' consumption decisions through a wealth effect. Additionally, international interest rate differentials affect exchange rates and consequently exports and imports. These various channels are collectively known as the monetary transmission mechanism. Consumption, investment and net exports are all important components of aggregate demand. Consequently, by influencing the general interest rate level, monetary policy can affect overall demand for goods and services in the economy and hence output and employment.[19] Changes in employment will over time affect wage setting, which again affects pricing and consequently ultimately inflation. The relation between employment (or unemployment) and inflation is known as the Phillips curve.[18]
For economies maintaining a fixed exchange rate system, determining the interest rate is also an important instrument of monetary policy as international capital flows are in part determined by interest rate differentials between countries.[20]
Interest rate setting in the United States

The Federal Reserve (often referred to as 'the Fed') implements monetary policy largely by targeting the federal funds rate (FFR). This is the rate that banks charge each other for overnight loans of federal funds, which are the reserves held by banks at the Fed. Until the global financial crisis in 2008, the Fed relied on open market operations, i.e. selling and buying securities in the open market to adjust the supply of reserve balances so as to keep the FFR close to the Fed's target.[21] However, since 2008 the actual conduct of monetary policy implementation has changed considerably, the Fed using instead various administered interest rates (i.e., interest rates that are set directly by the Fed rather than being determined by the market forces of supply and demand) as the primary tools to steer short-term market interest rates towards the Fed's policy target.[22]
Impact on savings and pensions
Financial economists such as World Pensions Council (WPC) researchers have argued that durably low interest rates in most G20 countries will have an adverse impact on the funding positions of pension funds as "without returns that outstrip inflation, pension investors face the real value of their savings declining rather than ratcheting up over the next few years".[23] Current interest rates in savings accounts often fail to keep up with the pace of inflation.[24]
From 1982 until 2012, most Western economies experienced a period of low inflation combined with relatively high returns on investments across all asset classes including government bonds. This brought a certain sense of complacency[citation needed] amongst some pension actuarial consultants and regulators, making it seem reasonable to use optimistic economic assumptions to calculate the present value of future pension liabilities.
Mathematical note
Because interest and inflation are generally given as percentage increases, the formulae above are (linear) approximations.
For instance,
is only approximate. In reality, the relationship is
so
The two approximations, eliminating higher order terms, are:
The formulae in this article are exact if logarithmic units are used for relative changes, or equivalently if logarithms of indices are used in place of rates, and hold even for large relative changes.
Zero rate policy
A so-called "zero interest-rate policy" (ZIRP) is a very low—near-zero—central bank target interest rate. At this zero lower bound the central bank faces difficulties with conventional monetary policy, because it is generally believed that market interest rates cannot realistically be pushed down into negative territory.
After the crisis of 2008, the Federal Reserve kept interest rates at zero for 12 years.[25]
Negative nominal or real rates
Nominal interest rates are normally positive, but not always. In contrast, real interest rates can be negative, when nominal interest rates are below inflation. When this is done via government policy (for example, via reserve requirements), this is deemed financial repression, and was practiced by countries such as the United States and United Kingdom following World War II (from 1945) until the late 1970s or early 1980s (during and following the Post–World War II economic expansion).[26][27] In the late 1970s, United States Treasury securities with negative real interest rates were deemed certificates of confiscation.[28]
On central bank reserves
A so-called "negative interest rate policy" (NIRP) is a negative (below zero) central bank target interest rate.
Theory
Given the alternative of holding cash, and thus earning 0%, rather than lending it out, profit-seeking lenders will not lend below 0%, as that will guarantee a loss, and a bank offering a negative deposit rate will find few takers, as savers will instead hold cash.[29]
Negative interest rates have been proposed in the past, notably in the late 19th century by Silvio Gesell.[30] A negative interest rate can be described (as by Gesell) as a "tax on holding money"; he proposed it as the Freigeld (free money) component of his Freiwirtschaft (free economy) system. To prevent people from holding cash (and thus earning 0%), Gesell suggested issuing money for a limited duration, after which it must be exchanged for new bills; attempts to hold money thus result in it expiring and becoming worthless. Along similar lines, John Maynard Keynes approvingly cited the idea of a carrying tax on money,[30] (1936, The General Theory of Employment, Interest and Money) but dismissed it due to administrative difficulties.[31] More recently, a carry tax on currency was proposed by a Federal Reserve employee (Marvin Goodfriend) in 1999, to be implemented via magnetic strips on bills, deducting the carry tax upon deposit, the tax being based on how long the bill had been held.[31]
It has been proposed that a negative interest rate can in principle be levied on existing paper currency via a serial number lottery, such as randomly choosing a number 0 through 9 and declaring that notes whose serial number end in that digit are worthless, yielding an average 10% loss of paper cash holdings to hoarders; a drawn two-digit number could match the last two digits on the note for a 1% loss. This was proposed by an anonymous student of Greg Mankiw,[30] though more as a thought experiment than a genuine proposal.[32]
Practice
Both the European Central Bank starting in 2014 and the Bank of Japan starting in early 2016 pursued the policy on top of their earlier and continuing quantitative easing policies. The latter's policy was said at its inception to be trying to "change Japan's 'deflationary mindset.'" In 2016 Sweden, Denmark and Switzerland—not directly participants in the Euro currency zone—also had NIRPs in place.[33]
Countries such as Sweden and Denmark have set negative interest on reserves—that is to say, they have charged interest on reserves.[34][35][36][37]
In July 2009, Sweden's central bank, the Riksbank, set its policy repo rate, the interest rate on its one-week deposit facility, at 0.25%, at the same time as setting its overnight deposit rate at −0.25%.[38] The existence of the negative overnight deposit rate was a technical consequence of the fact that overnight deposit rates are generally set at 0.5% below or 0.75% below the policy rate.[38][39] The Riksbank studied the impact of these changes and stated in a commentary report[40] that they led to no disruptions in Swedish financial markets.
On government bond yields

During the European debt crisis, government bonds of some countries (Switzerland, Denmark, Germany, Finland, the Netherlands and Austria) have been sold at negative yields. Suggested explanations include desire for safety and protection against the eurozone breaking up (in which case some eurozone countries might redenominate their debt into a stronger currency).[42]
On corporate bond yields
For practical purposes, investors and academics typically view the yields on government or quasi-government bonds guaranteed by a small number of the most creditworthy governments (United Kingdom, United States, Switzerland, EU, Japan) to effectively have negligible default risk. As financial theory would predict, investors and academics typically do not view non-government guaranteed corporate bonds in the same way. Most credit analysts value them at a spread to similar government bonds with similar duration, geographic exposure, and currency exposure. Through 2018 there have only been a few of these corporate bonds that have traded at negative nominal interest rates. The most notable example of this was Nestle, some of whose AAA-rated bonds traded at negative nominal interest rate in 2015. However, some academics and investors believe this may have been influenced by volatility in the currency market during this period.
See also
- Forward rate
- List of countries by central bank interest rates
- Macroeconomics
- Rate of return
- Short-rate model
- Spot rate
Notes
- ^ Fisher, Irving (1907). The Rate of Interest: Its Nature, Determination and Relation to Economic Phenomena. New York: The MacMillan Company. p. 8. ISBN 1578987458.
- ^ "Discount Rate Defined: How It's Used by the Fed and in Cash-Flow Analysis". Investopedia. Retrieved 2023-05-08.
- ^ "INSIGHT-Mild inflation, low interest rates could help economy". Reuters. 2 August 2011.
- ^ Sepehri, Ardeshir; Moshiri, Saeed (2004). "Inflation-Growth Profiles Across Countries: Evidence from Developing and Developed Countries". International Review of Applied Economics. 18 (2): 191–207. doi:10.1080/0269217042000186679. S2CID 154979402.
- ^ "Inflation : Finding the right balance" (PDF). Imf.org. Retrieved 8 January 2018.
- ^ "Finance & Development, June 2003 - Contents". Finance and Development – F&D.
- ^ "Finance & Development, March 2010 – Back to Basics". Finance and Development – F&D.
- ^ moneyextra.com Interest Rate History Archived 2008-10-16 at the Wayback Machine. Retrieved 2008-10-27
- ^ "UK interest rates lowered to 0.5%". BBC News. 5 March 2009.
- ^ (Homer, Sylla & Sylla 1996, p. 509)
- ^ Bundesbank. BBK – Statistics – Time series database Archived 2009-02-12 at the Wayback Machine. Retrieved 2008-10-27
- ^ worldeconomies.co.uk Zimbabwe currency revised to help inflation Archived 2009-02-11 at the Wayback Machine
- ^ (Homer, Sylla & Sylla 1996, p. 1)
- ^ Commonwealth Bank Why do Interest Rates Change? Archived 2014-02-26 at the Wayback Machine
- ^ Benchimol, J., 2014. Risk aversion in the Eurozone, Research in Economics, vol. 68, issue 1, pp. 39–56.
- ^ Interest rate spread (lending rate minus deposit rate, %) from World Bank. 2012
- ^ Negative Spread Law & Legal Definition, retrieved January 2013
- ^ a b Blanchard, Olivier; Amighini, Alessia; Giavazzi, Francesco (2017). "Monetary policy:a summing up". Macroeconomics: a European perspective (3rd ed.). Harlow London New York Boston San Francisco Toronto Sydney Dubai Singapore Hong Kong Tokyo Seoul Taipei New Delhi Cape Town São Paulo Mexico City Madrid Amsterdam Munich Paris Milan: Pearson. ISBN 978-1-292-08567-8.
- ^ "Federal Reserve Board - Monetary Policy: What Are Its Goals? How Does It Work?". Board of Governors of the Federal Reserve System. 29 July 2021. Retrieved 16 September 2023.
- ^ "Fixed exchange rate policy". Nationalbanken. Retrieved 16 September 2023.
- ^ "Open Market Operations". www.federalreserve.gov. Federal Reserve System. 26 July 2023. Retrieved 16 September 2023.
- ^ Ihrig, Jane; Weinbach, Gretchen C.; Wolla, Scott A. (September 2021). "Teaching the Linkage Between Banks and the Fed: R.I.P. Money Multiplier". research.stlouisfed.org. Federal Reserve Bank of St. Louis. Retrieved 16 September 2023.
- ^ M. Nicolas J. Firzli quoted in Sinead Cruise (4 August 2012). "Zero Return World Squeezes Retirement Plans". Reuters with CNBC. . Retrieved 5 Aug 2012.
- ^ thesavingsguy (2021-11-16). "Why You Can't Afford to use Savings Accounts for Saving - Ask The savings guy". Retrieved 2021-11-18.
- ^ Peter Schiff: The Latest Bank Bailout Is Another Nail in Capitalism’s Coffin
- ^ William H. Gross. "The Caine Mutiny Part 2 – PIMCO". Pacific Investment Management Company LLC.
- ^ "Financial Repression Redux (Reinhart, Kirkegaard, Sbrancia June 2011)" (PDF). Imf.org. Retrieved 8 January 2018.
- ^ Norris, Floyd (28 October 2010). "U.S. Bonds That Could Return Less Than Their Price". The New York Times.
- ^ Buiter, Willem (7 May 2009). "Negative interest rates: when are they coming to a central bank near you?". Financial Times blog.
- ^ a b c Mankiw, N. Gregory (18 April 2009). "It May Be Time for the Fed to Go Negative". The New York Times.
- ^ a b McCullagh, Declan (27 October 1999). "Cash and the 'Carry Tax'". WIRED. Retrieved 2011-12-21.
- ^ See follow-up blog posts for discussion: "Observations on Negative Interest Rates", 19 April 2009; "More on Negative Interest Rates", 22 April 2009; "More on Negative Interest Rates", 7 May 2009, all in Greg Mankiw's Blog: Random Observations for Students of Economics
- ^ Nakamichi, Takashi, Megumi Fujikawa and Eleanor Warnock, "Bank of Japan Introduces Negative Interest Rates" (possibly subscription-only)[permanent dead link], Wall Street Journal, January 29, 2016. Retrieved 2016-01-29.
- ^ Goodhart, C.A.E. (January 2013). "The Potential Instruments of Monetary Policy" (PDF). Financial Markets Group Paper (Special Paper 219). London School of Economics. 9–10. ISSN 1359-9151. Retrieved 13 April 2013.
{{cite journal}}: Cite journal requires|journal=(help) - ^ Blinder, Alan S. (February 2012). "Revisiting Monetary Policy in a Low-Inflation and Low-Utilization Environment". Journal of Money, Credit and Banking. 44 (Supplement s1): 141–146. doi:10.1111/j.1538-4616.2011.00481.x.
- ^ Thoma, Mark (August 27, 2012). "Would Lowering the Interest Rate on Excess Reserves Stimulate the Economy?". Economist's View. Retrieved 13 April 2013.
- ^ Parameswaran, Ashwin (2013-01-07). "On The Folly of Inflation Targeting In A World Of Interest Bearing Money". Macroeconomic Resilience. Retrieved 13 April 2013.
- ^ a b "Repo rate table". Sveriges Riksbank. Archived from the original on 5 February 2013. Retrieved 21 August 2013.
- ^ Ward, Andrew; Oakley, David (27 August 2009). "Bankers watch as Sweden goes negative". Financial Times. London. Archived from the original on 2022-12-10.
- ^ Beechey, Meredith; Elmér, Heidi (30 September 2009). "The lower limit of the Riksbank's repo rate" (PDF). Sveriges Riksbank. Retrieved 21 August 2013.
- ^ Figure. Irish yield curve
- ^ Wigglesworth, Robin (18 July 2012). "Schatz yields turn negative for first time". Financial Times. London. Archived from the original on 2022-12-10. Retrieved 2012-08-03.
References
- Homer, Sidney; Sylla, Richard Eugene; Sylla, Richard (1996). A History of Interest Rates. Rutgers University Press. ISBN 978-0-8135-2288-3. Retrieved 2008-10-27.

Practical C# and WPF for Financial Markets:
Advanced C#, WPF, and MVVM Programming for Quant Developers/Analysts and Individual Traders
Jack Xu -
Practical C# and WPF for Financial Markets provides a complete explanation of .NET programming in quantitative finance.

Practical Quantitative Finance with ASP.NET Core and Angular:
Building Ultra-Modern, Responsive Single-Page Web Applications for Quantitative Finance using ASP.NET Core and Angular.
Jack Xu -
Building Ultra-Modern, Responsive Single-Page Web Applications for Quantitative Finance using ASP.NET Core and Angular.

Financial Modelling: Theory, Implementation and Practice with MATLAB Source:
Daniel Wetterau - Jörg Kienitz
A unique contribution to the application of quantitative techniques to financial problems and programming using Matlab.

Quantitative Finance: An Object-Oriented Approach in C++:
Erik Schlögl -
Providing readers with a foundation in the key methods and models of quantitative finance. Keeping the material as self-contained as possible, the author introduces computational finance with a focus on practical implementation in C++.









